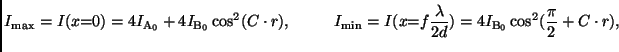Next: Gestirnsdurchmesser
Up: Objekte der Sterninterferometrie
Previous: Objekte der Sterninterferometrie
Contents
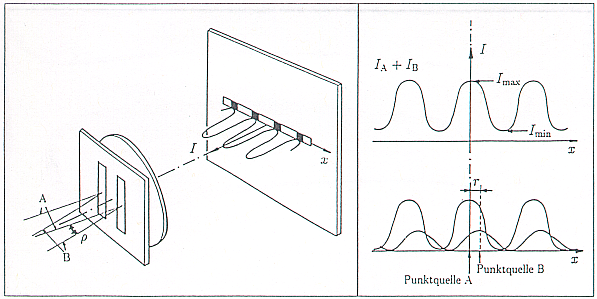
Bei der Beobachtung von Doppelsternen durch ein
MICHELSON-Sterninterferometer
entsteht in der Brennebene des Teleskops für jede Komponente des
Doppelsternsystems ein Interferenzstreifensystem (siehe Abb.
2 unten), wobei beide Streifensysteme entsprechend dem
Winkelabstand 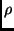 der Komponenten zueinander verschoben sind.
Da das Licht der Doppelsternkomponenten zueinander inkohärent ist, spielen
Interferenzerscheinungen keine Rolle und die Intensitätsverteilungen der
einzelnen Interferenzstreifensysteme addieren sich einfach zu einer resultierenden
Verteilung, welche auch wieder durch einen Wert von
der Komponenten zueinander verschoben sind.
Da das Licht der Doppelsternkomponenten zueinander inkohärent ist, spielen
Interferenzerscheinungen keine Rolle und die Intensitätsverteilungen der
einzelnen Interferenzstreifensysteme addieren sich einfach zu einer resultierenden
Verteilung, welche auch wieder durch einen Wert von  charakterisiert werden kann. Haben die Doppelsternkomponenten in der
Brennebene den Abstand
charakterisiert werden kann. Haben die Doppelsternkomponenten in der
Brennebene den Abstand
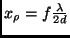 , d.h. das
zentrale Maximum des Streifensystems der einen Doppelsternkomponente
überlagert das dem zentralen Maximum angrenzende Minimum der zweiten
Komponente, wodurch der Streifenkontrast
, d.h. das
zentrale Maximum des Streifensystems der einen Doppelsternkomponente
überlagert das dem zentralen Maximum angrenzende Minimum der zweiten
Komponente, wodurch der Streifenkontrast  mehr oder weniger verschwindet
(die Tiefe des Minimums vom
mehr oder weniger verschwindet
(die Tiefe des Minimums vom  ist auch vom Helligkeitsverhältnis
der Doppelsternkomponenten abhängig). Bei einem Komponentenabstand von
ist auch vom Helligkeitsverhältnis
der Doppelsternkomponenten abhängig). Bei einem Komponentenabstand von
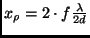 überlagert das zentrale Maximum
der einen Komponente das dem zentralen Maximum benachbarte Maximum der
zweiten Komponente, wodurch
überlagert das zentrale Maximum
der einen Komponente das dem zentralen Maximum benachbarte Maximum der
zweiten Komponente, wodurch 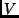 ein Maximum erreicht.
Bei
ein Maximum erreicht.
Bei
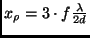 wird
wird 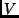 wieder minimal,
bei
wieder minimal,
bei
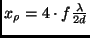 wieder maximal usw.
(der Spaltabstand
wieder maximal usw.
(der Spaltabstand 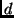 war bisher fest - folglich waren auch die
Interferenzstreifensysteme der einzelnen Doppelsternkomponenten unverändert).
Der kleinste
mit dem MICHELSON-Sterninterferometer auflösbare Winkelabstand
war bisher fest - folglich waren auch die
Interferenzstreifensysteme der einzelnen Doppelsternkomponenten unverändert).
Der kleinste
mit dem MICHELSON-Sterninterferometer auflösbare Winkelabstand 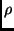 der Komponenten eines Doppelsternsystems beträgt also
der Komponenten eines Doppelsternsystems beträgt also
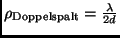 .
Vergleicht man diesen Wert mit dem
bei Beobachtung ohne Interferometeraufsatz auflösbaren Winkelabstand
.
Vergleicht man diesen Wert mit dem
bei Beobachtung ohne Interferometeraufsatz auflösbaren Winkelabstand
 erreichbaren Auflösungsvermögen, so ergibt sich
bei
erreichbaren Auflösungsvermögen, so ergibt sich
bei 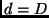 :
:
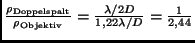 . Praktisch ist der Gewinn an Auflösung noch größer als
. Praktisch ist der Gewinn an Auflösung noch größer als
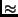 2,5.
Zur Bestimmung des Winkelabstandes
2,5.
Zur Bestimmung des Winkelabstandes 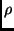 der Komponenten eines
Doppelsternsystems wird der Verlauf des Kontrastes
der Komponenten eines
Doppelsternsystems wird der Verlauf des Kontrastes 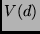 in Abhängigkeit
vom Spaltabstand bestimmt. Mit der Veränderung des Spaltabstandes
verändern sich diesmal jedoch die Interferenzstreifensysteme der einzelnen
Doppelsternkomponenten (mit wachsendem Spaltabstand werden die Abstände
der Streifen - Minima II. Klasse - geringer, d.h. die Zahl der Streifen
wächst, siehe dazu auch Abb. 3), der Abstand der Zentren der
Streifensysteme zueinander bleibt jedoch gleich.
in Abhängigkeit
vom Spaltabstand bestimmt. Mit der Veränderung des Spaltabstandes
verändern sich diesmal jedoch die Interferenzstreifensysteme der einzelnen
Doppelsternkomponenten (mit wachsendem Spaltabstand werden die Abstände
der Streifen - Minima II. Klasse - geringer, d.h. die Zahl der Streifen
wächst, siehe dazu auch Abb. 3), der Abstand der Zentren der
Streifensysteme zueinander bleibt jedoch gleich.
Die Intensitätsverteilung des Streifensystems, das im Falle des Lichtes
eines Doppelsternsystems hinter einem Doppelspalt entsteht (siehe
Abb. 4),
kann als Summe der in der
Brennebene um den Abstand 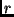 verschobenen Intensitätsverteilungen
der Interferenzstreifensysteme der einzelnen als punktförmig angenommenen
Komponenten A und B des Doppelsternsystems
(siehe Gleichung (1)) ausgedrückt werden:
verschobenen Intensitätsverteilungen
der Interferenzstreifensysteme der einzelnen als punktförmig angenommenen
Komponenten A und B des Doppelsternsystems
(siehe Gleichung (1)) ausgedrückt werden:
Dabei liegt die Doppelsternkomponente A auf der optischen Achse, die
Komponente B ist um den gesuchten Winkelabstand 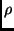 , welcher in
der Brennebene in
, welcher in
der Brennebene in 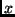 -Richtung als linearer Abstand
-Richtung als linearer Abstand 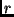 erscheint, zu A
verschoben (siehe Abb. 5), wobei gilt:
erscheint, zu A
verschoben (siehe Abb. 5), wobei gilt:
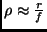 (
(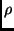 im Bogenmaß).
Gleichung (3) kann vereinfacht werden, wenn man annimmt,
daß
im Bogenmaß).
Gleichung (3) kann vereinfacht werden, wenn man annimmt,
daß 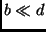 , d. h. wenn die die Streifen einhüllende Funktion
, d. h. wenn die die Streifen einhüllende Funktion
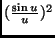 nur sehr langsam abfällt,
also in der Nähe des Zentrums
nur sehr langsam abfällt,
also in der Nähe des Zentrums 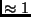 ist:
ist:
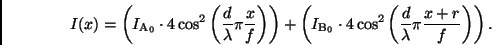 |
(4) |
Der Kontrast 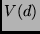 des Streifensystems beim Spaltabstand
des Streifensystems beim Spaltabstand 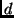 kann nun bestimmt werden, indem man zunächst für die in
(4) gegebene Intensitätsverteilung die Werte von
kann nun bestimmt werden, indem man zunächst für die in
(4) gegebene Intensitätsverteilung die Werte von
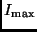 und
und 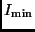 ermittelt und diese anschließend in
(2) einsetzt. Mit
ermittelt und diese anschließend in
(2) einsetzt. Mit
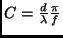 (
(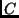 wird nur aus Übersichtsgründen eingeführt) und
wird nur aus Übersichtsgründen eingeführt) und
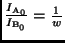 gilt:
gilt:
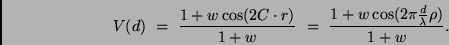 |
(5) |
Aus Abb. 5 wird ersichtlich, daß eine
Winkelabstandsbestimmung von Doppelsternen praktisch nur für solche
Objekte mit geringem Helligkeitsunterschied 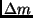 möglich ist, da nur in
diesen Fällen Kontrastunterschiede deutlich sichtbar werden
(
möglich ist, da nur in
diesen Fällen Kontrastunterschiede deutlich sichtbar werden
(
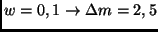 mag,
mag,
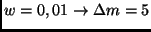 mag).
Im Falle beobachtbarer
Kontrastunterschiede kann dann aber neben der Abstandsinformation mit Hilfe
von
mag).
Im Falle beobachtbarer
Kontrastunterschiede kann dann aber neben der Abstandsinformation mit Hilfe
von 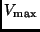 und
und  auch auf das Intensitätsverhältnis
auch auf das Intensitätsverhältnis 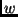 geschlossen werden:
geschlossen werden:




Next: Gestirnsdurchmesser
Up: Objekte der Sterninterferometrie
Previous: Objekte der Sterninterferometrie
Contents
Juergen Weiprecht
2002-10-29