Next: Mittlerer Fehler und statistische
Up: Rechnerische Erfassung zufälliger Fehler
Previous: Arithmetisches Mittel
Contents
Vielfach läßt sich eine zu ermittelnde Größe nicht direkt bestimmen. Sie
muß vielmehr indirekt aus einer Anzahl 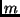 von unabhängig voneinander zu
messenden Größen erschlossen werden. Der Einfachheit wegen sei zunächst
angenommen, daß
von unabhängig voneinander zu
messenden Größen erschlossen werden. Der Einfachheit wegen sei zunächst
angenommen, daß 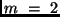 sei, daß also die zu ermittelnde Größe
sei, daß also die zu ermittelnde Größe 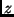 von
zwei unabhängigen Beobachtungsgrößen
von
zwei unabhängigen Beobachtungsgrößen 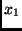 und
und 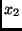 abhängt:
abhängt:
 |
(16) |
Für 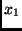 mögen
mögen 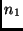 , für
, für 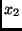
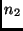 Beobachtungen vorliegen. Damit
berechnen sich die Mittelwerte zu
Beobachtungen vorliegen. Damit
berechnen sich die Mittelwerte zu
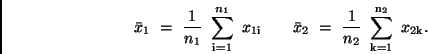 |
(17) |
Mit den scheinbaren Fehlern
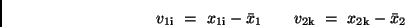 |
(18) |
erhält man für die Standardabweichungen
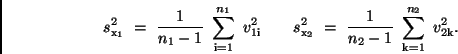 |
(19) |
Setzt man die Werte 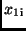 und
und 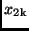 in (16) ein, so erhält
man mit
(18)
in (16) ein, so erhält
man mit
(18)
Die Taylor-Reihenentwicklung, die man nach dem linearen Glied abbricht,
ergibt
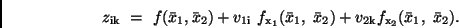 |
(20) |
Dabei bedeuten
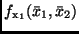 und
und
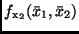 die partiellen Ableitungen von
die partiellen Ableitungen von
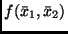 genommen für die Werte
genommen für die Werte
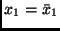 und
und
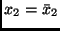 .
Zur Ermittlung des arithmetischen Mittels
.
Zur Ermittlung des arithmetischen Mittels 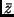 bestimmt man zunächst
bestimmt man zunächst
und danach
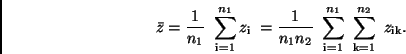 |
(21) |
Dies läßt sich mit (20) umschreiben in
woraus sich
und unter Beachtung von (13)
 |
(22) |
ergibt. Den gesuchten Mittelwert 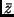 von
von 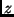 erhält man also einfach
dadurch, daß man in
erhält man also einfach
dadurch, daß man in 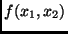 die Mittelwerte
die Mittelwerte 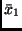 und
und
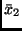 einsetzt.
Zur Berechnung der Standardabweichung
einsetzt.
Zur Berechnung der Standardabweichung 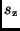 der
der 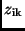 -Werte
definiert
man analog zu (10) scheinbare Fehler
-Werte
definiert
man analog zu (10) scheinbare Fehler
Damit erhält man nach (15)
und unter Beachtung von (20) und (22)
Nach der Ausmultiplikation ergibt sich, wenn man
woraus man
erhält. Bei genügend großen 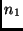 und
und 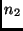 kann man
kann man
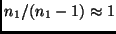 und
und
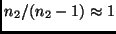 setzen, so daß sich unter Beachtung von
(13)
setzen, so daß sich unter Beachtung von
(13)
ergibt, was sich mit (19) endgültig in
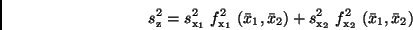 |
(23) |
umschreiben läßt. Damit ist die Rechenvorschrift zur Ermittlung der
Standardabweichung 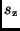 aus den Standardabweichungen
aus den Standardabweichungen 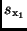 und
und
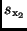 gefunden. Die Beziehung (23) zeigt, wie sich Fehler in den
Beobachtungsgrößen
gefunden. Die Beziehung (23) zeigt, wie sich Fehler in den
Beobachtungsgrößen 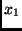 und
und 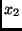 auf die Unsicherheit der gesuchten
Größe
auf die Unsicherheit der gesuchten
Größe 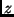 auswirken. Dieses Fehlerfortpflanzungsgesetz für die
Standardabweichungen läßt sich sofort auf den Fall erweitern, daß die
Größe
auswirken. Dieses Fehlerfortpflanzungsgesetz für die
Standardabweichungen läßt sich sofort auf den Fall erweitern, daß die
Größe 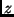 von
von 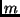 Beobachtungsgrößen
Beobachtungsgrößen
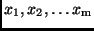 abhängt,
abhängt,
 |
(24) |
Aus (22) folgt
 |
(25) |
und aus (23)
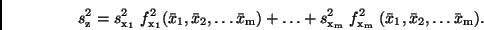 |
(26) |
Aus (23) bzw. (26) läßt sich abschätzen, welcher Summand (welche
Beobachtungsgröße) den Hauptbeitrag zum Gesamtfehler leistet. Man muß
versuchen, die Unsicherheit speziell dieser Beobachtungsgröße - etwa durch
eine erhöhte Anzahl von Beobachtungen - möglichst herabzudrücken.




Next: Mittlerer Fehler und statistische
Up: Rechnerische Erfassung zufälliger Fehler
Previous: Arithmetisches Mittel
Contents
Juergen Weiprecht
2002-10-29
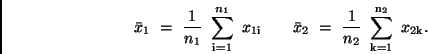
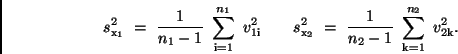

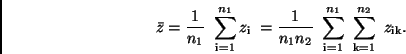
![\begin{displaymath}
\bar{z} = \frac{1}{n_1 n_2} \ \sum_{\rm i=1}^{n_1} \
\sum_...
..., \bar{x}_2) +
v_{\rm 2k} f (\bar{x}_1, \bar{x}_2) \right] ,
\end{displaymath}](img1649.png)
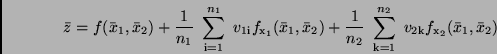
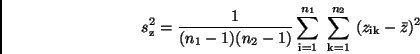
![\begin{displaymath}
s_{\rm z}^{2} = \frac{1}{(n_1 - 1)(n_2 - 1)} \ \sum_{\rm i=...
... v_{\rm 2k} f_{\rm x_2} \
(\bar{x}_1, \bar{x}_2) \right] ^2.
\end{displaymath}](img1659.png)
![\begin{displaymath}
s_{\rm z}^{2} = \frac{1}{(n_1 - 1)(n_2 -1)} \ \sum_{\rm i=1...
...m x_1}
f_{\rm x_2} + v_{\rm 2k}^2 f_{\rm x_2}^2 \
\right] ,
\end{displaymath}](img1661.png)
![\begin{displaymath}
s_{\rm z}^{2} = \frac{1}{(n_1 - 1)(n_2 - 1)} \left[ n_2 \
...
...um_{\rm k=1}^{n_2} \
v_{\rm 2k}^2 \ f_{\rm x_2}^2 \
\right]
\end{displaymath}](img1662.png)